算法模板 - 二叉树遍历

二叉树遍历介绍
递归法
迭代法
Morris 法
题目
番外

# 二叉树遍历介绍

二叉树的三大遍历：前序遍历、中序遍历、后序遍历。

树的实体类，下面会用到：

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode() {}
    public TreeNode(int val) { this.val = val; }
    public TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

# 递归法

# 前序遍历

public static void preOrderRecur(TreeNode root) {
    if (root == null) {
        return;
    }
    System.out.print("前序遍历，这里应该存节点，如：list.add(root)");
    // 遍历左节点 
    preOrderRecur(root.left);
    // 遍历右节点 
    preOrderRecur(root.right);
}

1
2
3
4
5
6
7
8
9
10

# 中序遍历

public static void preOrderRecur(TreeNode root) {
    if (root == null) {
        return;
    }
    // 遍历左节点 
    preOrderRecur(root.left);
    System.out.print("中序遍历，这里应该存节点，如：list.add(root)");
    // 遍历右节点 
    preOrderRecur(root.right);
}

1
2
3
4
5
6
7
8
9
10

# 后序遍历

public static void postOrderRecur(TreeNode root) {
    if (root == null) {
        return;
    }
    // 遍历左节点 
    postOrderRecur(root.left);
    // 遍历右节点 
    postOrderRecur(root.right);
    System.out.print("后序遍历，这里应该存节点，如：list.add(root)");
}

1
2
3
4
5
6
7
8
9
10

# 总结

可以看出，三大遍历的存值位置发生变化。

# 迭代法

# 前序遍历

本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用 Stack 来模拟系统栈。

首先我们应该创建一个 Stack 用来存放节点，首先我们想要打印根节点的数据，此时 Stack 里面的内容为空，所以我们优先将头结点加入 Stack，然后打印。

之后我们应该先打印左子树，然后右子树。所以先加入 Stack 的就是右子树，然后左子树。

此时你能得到的流程如下:

代码：

public static void preOrderIteration(TreeNode root) {
	if (root == null) {
		return;
	}
	Stack<TreeNode> stack = new Stack<>();
	stack.push(root);
	while (!stack.isEmpty()) {
		TreeNode node = stack.pop();
		System.out.print("前序遍历，这里应该存节点，如：list.add(node)");
		if (node.right != null) {
			stack.push(node.right);
		}
		if (node.left != null) {
			stack.push(node.left);
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 中序遍历

同理创建一个 Stack，然后按左 -> 中 -> 右的顺序输出节点。

尽可能的将这个节点的左子树压入 Stack，此时栈顶的元素是最左侧的元素，其目的是找到一个最小单位的子树（也就是最左侧的一个节点），并且在寻找的过程中记录了来源，才能返回上层,同时在返回上层的时候已经处理完毕左子树了。

当处理完最小单位的子树时，返回到上层处理了中间节点。（如果把整个左中右的遍历都理解成子树的话，就是处理完左子树 -> 中间（就是一个节点） -> 右子树）

如果有右节点，其也要进行中序遍历。当整个左子树退栈的时候这个时候输出了该子树的根节点 2，之后输出中间节点 1。然后处理根节点为 3 右子树。

代码：

public static void inOrderIteration(TreeNode root) {
	if (root == null) {
		return;
	}
	TreeNode cur = root;
	Stack<TreeNode> stack = new Stack<>();
	while (!stack.isEmpty() || cur != null) {
		while (cur != null) {
			stack.push(cur);
			cur = cur.left;
		}
		TreeNode node = stack.pop();
		System.out.print("中序遍历，这里应该存节点，如：list.add(node)");
		if (node.right != null) {
			cur = node.right;
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 后序遍历

用一个指针 cur 标记当前退出的节点是什么。

后序遍历的过程中在遍历完左子树跟右子树 cur 都会回到根结点。所以当前不管是从左子树还是右子树回到根结点都不应该再操作了，应该退回上层。

如果是从右边再返回根结点，应该回到上层。

public static void postOrderIteration2(TreeNode root) { 
	if (root == null) {
		return;
	}
	TreeNode cur = root;
	Stack<TreeNode> stack = new Stack<>();
	stack.push(root);
	while (!stack.isEmpty()) {
		TreeNode peek = stack.peek();
		if (peek.left != null && peek.left != cur && peek.right != cur) {
			stack.push(peek.left);
		} else if (peek.right != null && peek.right != cur) {
			stack.push(peek.right);
		} else {
            TreeNode node = stack.pop();
			System.out.print("后序遍历，这里应该存节点，如：list.add(node)");
			cur = peek;
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Morris 法

Morris 遍历使用二叉树节点中大量指向 null 的指针，由 Joseph Morris 于 1979 年发明。

时间复杂度：O(n)

额外空间复杂度：O(1)

首先了解 Morris 的通用解法过程。

前驱节点 (predecessor) 中序遍历时的前一个节点。

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其前序遍历规则总结如下：

新建临时节点，令该节点为 cur
如果当前节点的左子节点为空，将当前节点加入答案，并遍历当前节点的右子节点
如果当前节点的左子节点不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点：
- 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为当前节点。然后将当前节点加入答案，并将前驱节点的右子节点更新为当前节点。当前节点更新为当前节点的左子节点
- 如果前驱节点的右子节点为当前节点，将它的右子节点重新设为空。当前节点更新为当前节点的右子节点
重复步骤 2 和步骤 3，直到遍历结束

这样我们利用 Morris 遍历的方法，前序遍历该二叉树，即可实现线性时间与常数空间的遍历。

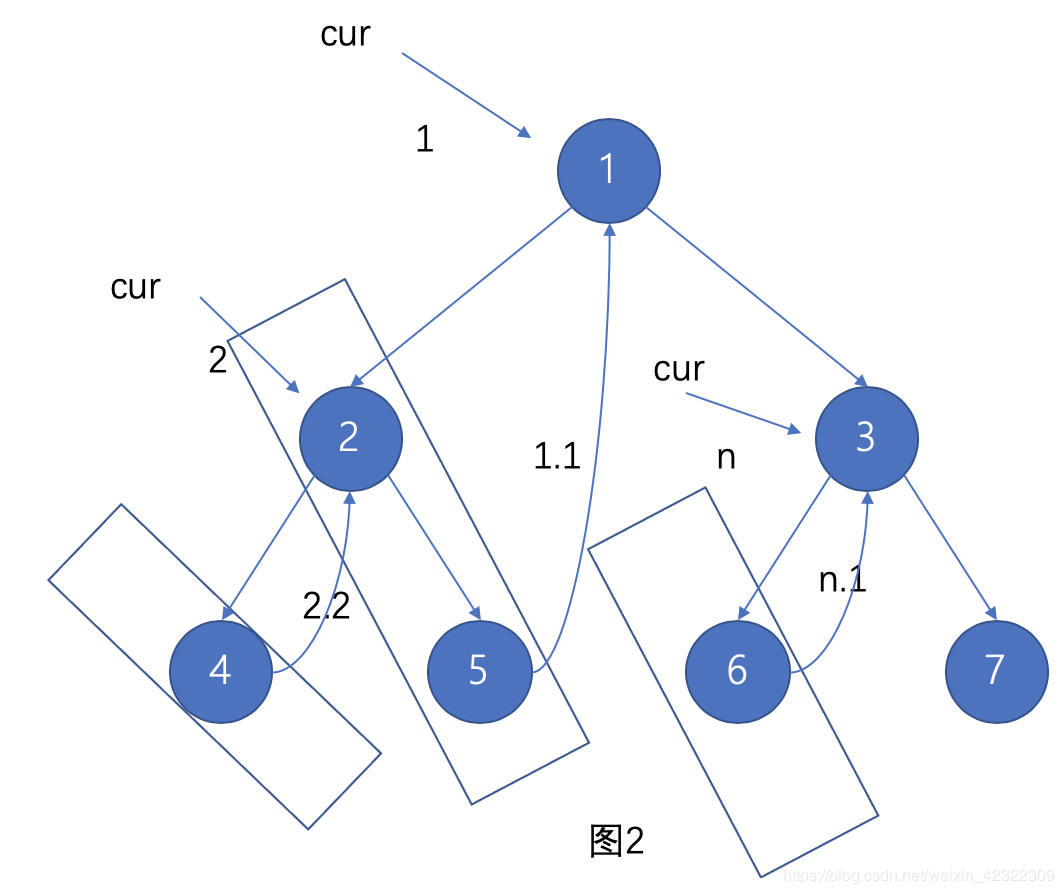
Morris 的整体思路就是将以某个根结点开始，找到它左子树的最右侧节点之后与这个根结点进行连接。

我们可以从图 2 看到：

当 cur 等于 1 时，其左节点 2 的最右侧节点 5 与 cur = 1 进行连接
当 cur 等于 2 时，其左节点 4 的最右侧节点 4（本身）与 cur = 2 进行连接

如果这么连接之后，cur 这个指针是可以完整的从一个节点顺着下一个节点遍历，将整棵树遍历完毕，直到 7 这个节点右侧没有指向。

public static void preOrderMorris(TreeNode root) {
	if (root == null) {
		return;
	}
	TreeNode cur1 = root; // 当前开始遍历的节点
	TreeNode cur2 = null; // 记录当前结点的左子树
	while (cur1 != null) {
		cur2 = cur1.left;
		if (cur2 != null) {
			while (cur2.right != null && cur2.right != cur1) { // 找到当前左子树的最右侧节点，且这个节点应该在指向根结点之前，否则整个节点又回到了根结点。
				cur2 = cur2.right;
			}
			if (cur2.right == null) { // 这个时候如果最右侧这个节点的右指针没有指向根结点，创建连接然后往下一个左子树的根结点进行连接操作。
				cur2.right = cur1;
				cur1 = cur1.left;
				continue;
			} else { // 当左子树的最右侧节点有指向根结点，此时说明我们已经回到了根结点并重复了之前的操作，同时在回到根结点的时候我们应该已经处理完左子树的最右侧节点了，把路断开。
				cur2.right = null;
			}
		}
		cur1 = cur1.right; // 一直往右边走，参考图
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 前序遍历

在某个根结点创建连线的时候打印。因为我们是顺着左边的根节点来创建连线，且创建的过程只有一次
打印某些自身无法创建连线的节点，也就是叶子节点

public static void preOrderMorris(TreeNode root) {
    if (root == null) {
        return;
    }
    TreeNode cur1 = root;
    TreeNode cur2 = null;
    while (cur1 != null) {
        cur2 = cur1.left;
        if (cur2 != null) {
            while (cur2.right != null && cur2.right != cur1) {
                cur2 = cur2.right;
            }
            if (cur2.right == null) {
                cur2.right = cur1;
                System.out.print("前序遍历，这里应该存节点，如：list.add(cur1)");
                cur1 = cur1.left;
                continue;
            } else {
                cur2.right = null;
            }
        } else {
            System.out.print("前序遍历，这里应该存节点，如：list.add(cur1)");
        }
        cur1 = cur1.right;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 中序遍历

从最左侧开始顺着右节点打印。也就是在将cu1切换到上层节点的时候。

public static void inOrderMorris(TreeNode v) {
	if (root == null) {
		return;
	}
	TreeNode cur1 = root;
	TreeNode cur2 = null;
	while (cur1 != null) {
		cur2 = cur1.left;
		// 构建连接线
		if (cur2 != null) {
			while (cur2.right != null && cur2.right != cur1) {
				cur2 = cur2.right;
			}
			if (cur2.right == null) {
				cur2.right = cur1;
				cur1 = cur1.left;
				continue;
			} else {
				cur2.right = null;
			}
		}
		System.out.print("中序遍历，这里应该存节点，如：list.add(cur1)");
		cur1 = cur1.right;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 后序遍历

当我们到达最左侧，也就是左边连线已经创建完毕了。

打印 4
打印 5 2
打印 6
打印 7 3 1

我们将一个节点的连续右节点当成一个单链表来看待。

当我们返回上层之后，也就是将连线断开的时候，打印下层的单链表。

比如返回到　２，此时打印　４
比如返回到　１，此时打印　５　２
比如返回到　３，此时打印　６

那么我们只需要将这个单链表逆序打印就行了，下文也给出了单链表逆序代码

这里不应该打印当前层，而是下一层，否则根结点会先与右边打印。

public static void postOrderMorris(TreeNode root) {
    if (root == null) {
        return;
    }
    TreeNode cur1 = root; // 遍历树的指针变量
    TreeNode cur2 = null; // 当前子树的最右节点
    while (cur1 != null) {
        cur2 = cur1.left;
        if (cur2 != null) {
            while (cur2.right != null && cur2.right != cur1) {
                cur2 = cur2.right;
            }
            if (cur2.right == null) {
                cur2.right = cur1;
                cur1 = cur1.left;
                continue;
            } else {
                cur2.right = null;
                postMorrisPrint(cur1.left);
            }
        }
        cur1 = cur1.right;
    }
    postMorrisPrint(root);
}
// 打印函数
public static void postMorrisPrint(TreeNode root) {
    TreeNode reverseList = postMorrisReverseList(root);
    TreeNode cur = reverseList;
    while (cur != null) {
        System.out.print("后序遍历，这里应该存节点，如：list.add(cur)");
        cur = cur.right;
    }
    postMorrisReverseList(reverseList);
}
// 翻转单链表
public static TreeNode postMorrisReverseList(TreeNode root) {
    TreeNode cur = root;
    TreeNode pre = null;
    while (cur != null) {
        TreeNode next = cur.right;
        cur.right = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

# 题目

# 前序遍历

题目来自：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/。

给定二叉树的根节点 root ，返回它节点值的前序遍历。

递归法

public class PreorderTraversal {

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        repeat(root, list);
        return list;
    }
    
    public void recursion(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        list.add(root.val);
        repeat(root.left, list);
        repeat(root.right, list);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

迭代法 1

先遍历树节点的左侧，遍历一次，则添加放集合（存值）和栈（存节点）里，当左侧节点为 null 时，代表已经到底了，则从栈里拿出上一个节点，从其右节点出发，继续遍历该右节点的左侧节点。

public class PreorderTraversa {
    public List<Integer> preorderTraversal1(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new ArrayList<>();
        while (root != null || !stack.isEmpty()) {
           if(root != null) {
               list.add(root.val);
               stack.push(root);
               root = root.left;
           }else {
               root = stack.pop();
               root = root.right;
           }
        }
        return list;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

迭代法 2

将一个节点添加到集合时，同时将这个节点的右节点先添加到栈里，再添加左节点，到底时，因为栈的特性，栈的上面优先为最下面的右节点，也就是先把一个节点的左侧节点都添加完，再添加右侧节点

public class PreorderTraversal {

    public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new ArrayList<>();
        if (root == null) {
            return list;
        }
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            list.add(node.val);
            if (node.right != null) {
                stack.push(node.right);
            }
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        return list;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

Morris 法

public class PreorderTraversal {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }
        TreeNode p1 = root;
        TreeNode p2 = null;
        while (p1 != null) {
            p2 = p1.left;
            if (p2 != null) {
                while (p2.right != null && p2.right != p1) {
                    p2 = p2.right;
                }
                if (p2.right == null) {
                    res.add(p1.val);
                    p2.right = p1;
                    p1 = p1.left;
                    continue;
                } else {
                    p2.right = null;
                }
            } else {
                res.add(p1.val);
            }
            p1 = p1.right;
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 中序遍历

题目来自：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/。

给定一个二叉树的根节点 root ，返回它的 中序遍历 。

递归法

public class InorderTraversal {

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        recursion(root, res);
        return res;
    }

    public void recursion(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        // 遍历左节点到最下面
        recursion(root.left, res);
        res.add(root.val);
        // 遍历右节点到最下面
        recursion(root.right, res);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

迭代法

public class InorderTraversal {

    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new ArrayList<>();
        while (root != null || !stack.isEmpty()) {
            // 栈存所有左节点
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            // 首先弹出最下面的左节点
            root = stack.pop();
            list.add(root.val);
            // 进入到右节点，在该右节点继
            root = root.right;
        }
        return list;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Morris 中序遍历

public class InorderTraversal {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        TreeNode predecessor = null;

        while (root != null) {
            if (root.left != null) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root.left;
                while (predecessor.right != null && predecessor.right != root) {
                    predecessor = predecessor.right;
                }
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor.right == null) {
                    predecessor.right = root;
                    root = root.left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.add(root.val);
                    predecessor.right = null;
                    root = root.right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.add(root.val);
                root = root.right;
            }
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 后序遍历

题目来：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/。

给定一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

递归法

public class PostorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        recursion(root, res);
        return res;
    }

    public void recursion(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        // 遍历左节点到最下面
        recursion(root.left, res);
        // 遍历右节点到最下面
        recursion(root.right, res);
        res.add(root.val);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

迭代法 1

根据中序遍历衍生而来。

与中序的不同之处在于：

中序遍历中，从栈中弹出的节点，其左子树是访问完了，可以直接访问该节点，然后接下来访问右子树
后序遍历中，从栈中弹出的节点，我们只能确定其左子树肯定访问完了，但是无法确定右子树是否访问过

因此，我们在后序遍历中，引入了一个 prev 来记录历史访问记录。

当访问完一棵子树的时候，我们用 prev 指向该节点。
这样，在回溯到父节点的时候，我们可以依据 prev 是指向左子节点，还是右子节点，来判断父节点的访问情况

public class PostorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        Stack<TreeNode> stack = new Stack<>();
        // 由于在某颗子树访问完成以后，接着就要回溯到其父节点去
        // 因此可以用 prev 来记录访问历史，在回溯到父节点时，可以由此来判断，上一个访问的节点是否为右子树
        TreeNode prev = null;
        while(root != null || !stack.isEmpty()){
            while(root != null){
                stack.push(root);
                root = root.left;
            }
            // 从栈中弹出的元素，左子树一定是访问完了x的
            root = stack.pop();
            // 现在需要确定的是是否有右子树，或者右子树是否访问过
            // 如果没有右子树，或者右子树访问完了，也就是上一个访问的节点是右子节点时，说明可以访问当前节点
            if(root.right == null || prev == root.right){
                ans.add(root.val);
                // 更新历史访问记录，这样回溯的时候父节点可以由此判断右子树是否访问完成
                prev = root;
                // 防止上面继续 while
                root = null;
            }else{
                // 如果右子树没有被访问，那么将当前节点压栈，访问右子树
                stack.push(root);
                root = root.right;
            }
        }
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

迭代法 2

根据前序遍历衍生而来，因为后续遍历就是前序遍历的倒过来版本，所以添加的时候，往集合的初始位置添加即可。

public class PostorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new java.util.ArrayList<>();
        if (root == null) {
            return list;
        }
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            list.add(0, node.val); // 初始位置
            if (node.left != null) {
                stack.push(node.left);
            }
            if (node.right != null) {
                stack.push(node.right);
            }
        }
        return list;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Morris 法

public class PostorderTraversal {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }
        TreeNode p1 = root, p2 = null;
        while (p1 != null) {
            p2 = p1.left;
            if (p2 != null) {
                while (p2.right != null && p2.right != p1) {
                    p2 = p2.right;
                }
                if (p2.right == null) {
                    p2.right = p1;
                    p1 = p1.left;
                    continue;
                } else {
                    p2.right = null;
                    addPath(res, p1.left);
                }
            }
            p1 = p1.right;
        }
        addPath(res, root);
        return res;
    }

    public void addPath(List<Integer> res, TreeNode node) {
        int count = 0;
        while (node != null) {
            ++count;
            res.add(node.val);
            node = node.right;
        }
        int left = res.size() - count, right = res.size() - 1;
        while (left < right) {
            int temp = res.get(left);
            res.set(left, res.get(right));
            res.set(right, temp);
            left++;
            right--;
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

内容来自：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/leetcodesuan-fa-xiu-lian-dong-hua-yan-shi-xbian-2/。

题目来自力扣。

# 番外

将字符串转为树节点。

字符串不带 null

当 data = "1,2"，输出 [1,null,2]，因为 1 < 2，所以 root = 1，root.left = null，root.right = 2。

public class Codec {

    public TreeNode deserialize(String data) {
        if (data == null) {
            return null;
        }
        String[] nodes = data.split(",");
        return dfs(0, nodes.length - 1, nodes);
    }
    // start 为遍历的起点，length 为遍历的长度，nodes 为遍历的数据
    TreeNode dfs(int start, int length, String[] nodes) {
        if (start > length) {
            return null;
        }
        int j = start + 1;
        int t = Integer.parseInt(nodes[start]);
        TreeNode ans = new TreeNode(t);
        // 计算左子树的长度 j
        while (j <= length && Integer.parseInt(nodes[j]) <= t) {
            j++;
        }
        // 左子树的长度为遍历的长度
        ans.left = dfs(start + 1, j - 1, nodes);
        // 左子树的长度为起点，字符串的长度为终点
        ans.right = dfs(j, length, nodes);
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

字符串自带 null

如果 data = "1,null,2"，输出 [1,null,2]。

public class Codec {

    public TreeNode deserialize(String data) {
        if (data == null) {
            return null;
        }
        String[] nodes = data.split(",");
        return dfs(0, nodes);
    }
    public TreeNode dfs(int index, String[] nodes) {
        if (nodes.length - 1 < index) {
            return null;
        }
        // 字符串的 null 在树节点直接添加为 null
        if(nodes[index].equals("null")) {
            return null;
        }
        TreeNode root = new TreeNode(Integer.parseInt(nodes[index]));
        root.left = dfs(index * 2 + 1, nodes);
        root.right = dfs(index * 2 + 2, nodes);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

编辑此页

#算法

更新时间: 2023/10/23, 10:58:52

← 算法模板 - 滑动窗口模板算法模板 - 单调栈→